Loop Invariants

Round and round and round it goes, and where it stops... With loop invariants, you'll know. And they'll help get the logic right, too.

The vast majority of the time, loops are easy to write. You have a termination condition, and something to do repeatedly until that condition is met.

Every now and then, though, you come across the loop that just won’t behave. You find yourself adding one to a value as a possible fix. Or changing < to <=. You end up getting it working, but the process just doesn’t feel right.

In those cases, I fall back on using loop invariants to inform my coding.

Let’s Start With Assertions

Not exactly rocket science. We assign a value to a variable, and (assuming the program is still running) immediately after the assignment the variable will have that value.

We can express that assertion as a predicate. By convention, we’ll write the predicate between braces. This isn’t executable code, so it’s also in a comment.

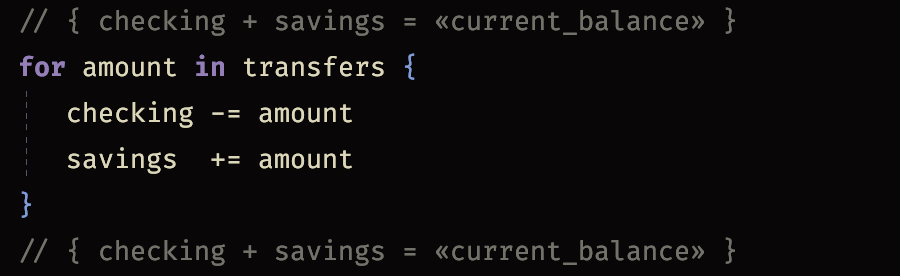
Let’s make it more interesting. We’ll transfer $100 from checking to savings.

I added an assertion before the code that claimed that the sum of the amounts in the checking and savings accounts is some number I called «current_balance». The guillemots just mean that this is a value in the land of assertions, but doesn’t correspond to an explicit value in the code.

The identical assertion appears after the two lines of code. Suddenly, this gets more interesting; we’re asserting that our code doesn’t change the total amount of money in the world.

Up one more notch:

This starts to get powerful: if the before assertion (the precondition) is true, then we can also claim that the postcondition is true.

(At this point, I’m cheating a little: we can eyeball this code and verify that the two lines will maintain the precondition. It is possible (and fairly easy) to prove this to be the case, but that’s not where I want to take this article. I’m also introducing the pseudo-variable current_balance, while a real proof would express the balance in terms of the values of the two real variables. I think that’s an OK thing to do: we’re not producing formal proofs of correctness; we’re looking for help designing our code.)

Take it a step further:

If we put our two lines of code in a loop, something interesting happens. Because the precondition is the same as the postcondition, and because none of the state mentioned in these predicates changes between the end of one iteration and the start of the next, we can make the assertions more general:

In this particular case, we can move the assertions outside the loop, and express a higher level fact about our code.

And We Discover Invariants

For our original two lines of code, we found a predicate, an assertion, that is true both as a precondition and as a postcondition. In a slightly more mathematical way, we could write this as

\(\{P\}\ \textit{code}\ \{P\}\)

If predicate P is true before code executes, then it will be true after as well.

We call P an invariant of the code.

Make Invariants More Loopy

If {P} code {P}, then {P} code code code {P} must also be true. That’s why we could safely move the predicates out of the for loop.

We can take it a step further. Think of a while loop:

while test do code

If P is true before the loop, it will also be true after it. But we know one more thing: after the loop, test will be false. This means we can write

\(\{P\}\ \textsf{while}\, \textit{test} \, \textsf{do} \, \textit{code}\ \{P \land \neg\, \textit{test}\}\)

That small addition of ¬ test can be significant when it comes to working out if the code we write is correct.

Some Examples

Let’s sum a list of values.

The intent of the code is to find a «result» which is ∑values, so we could try a predicate such as { «result» = ∑values }. While true, it doesn’t actually tell us anything; it’s just a tautology.

So let’s look at the body of the loop, and work out what gets changed.

Initially, the «result» is just the sum of the values in our list. By the end of the first iteration, the total is now 5 (the first element of the list) and we’ve effectively consumed the element at index zero; the list we still have to process is [ 2, 7, -6 ]. The sum of those three elements is 3.

After the next iteration, the total is 7 and the list is [7, -6], with a sum of 1.

There’s our invariant: { total + ∑values[i..] = «result» }. Each time around the loop, we transfer a value from the list to the total. OK, you might be thinking. Big deal. But this is obviously a simple, contrived, example. But it still has an interesting twist.

The loop terminates when i >= values.length. This means that ∑values[i..] will be 0. Our invariant tells us that { total + ∑values[i..] = «result» }, which means that { total + 0 = «result» }; we’ve proven that if our invariant is true, then this loop does indeed sum the values.

Slightly More Complicated

Run-length encoding (RLE) is a compression technique which takes runs of the same value and replaces them with a single value and a count. It works well when compressing data which contains many of these runs: the image of an icon, for example, might be largely white cells, and would compress well. Although superseded by LZ compression (which works the same way, but compresses repeated sequences of values), RLE still has uses today.

A simple RLE implementation might take the input

\([ 1, 1, 1, 3, 2, 2, 2, 2 ]\)

and return

\([ \ [1,3],\ [3,1],\ [2,4]\ ]\)

Although the algorithm is straightforward, the implementation is a little tricky: it’s easy to miss edge cases. So let’s see if loop invariants might help.

We’ll assume that we iterate over the input values, building the result as we go, so the overall structure is

Our job is to work out an invariant for that inner block.

I like to start by tabulating the values of a sample run. In this case the only variables we care about are the values and the result.

You notice I put the result on the left and the values on the right. That’s because our algorithm takes values from the front of the list and builds the result by appending to it.

On the first line, the result is empty and the values variable contains our initial list.

At the end of the algorithm, the result holds the encoded list, and the values list is empty.

Is there a predicate that’s true for both of these cases?

Let’s assume we have a function in our predicate language that decodes an RLE value into a flat list. In that case, and assuming + is array concatenation, we have

\(\textit{decode}(\textit{result}) + \textit{values} = «\textit{original_list»}\)

Now all we have to do is verify it is also true for each step.

Let’s pick a random iteration. At the start of the fourth time around the loop, our result is [{1,3}] and the remaining values are [3,2,2,2,2]. Concatenate the decoded result with those values, and you get the original list. The body of the loop then runs, and we get [{1,3}, {3,1}] and [2,2,2,2]. The predicate still holds.

Now our job is to write a block of code that honors that invariant. That block will have access to the current result, the list of values, and the index of the value in that list that is being processed.

Let’s start by fetching the next value:

At this point, we’ve broken the invariant: we’ve taken a value off the values array but have not updated the result. The invariant is forcing us to look at the result next.

To make the invariant correct, we need to append the value to the result, but the result is currently empty. A single value is represented by [ value, 1 ], so

Have we satisfied the invariant? When we decode the result, we’ll get [ value ], and when we append the remainder of the values we get the original list, so yes.

If the result list isn’t empty, then we have two choices. If the value in the last entry is the same as this new value, we just update that entry’s count.

How about the invariant? We’ve taken a value off the values list, but we’ve effectively added it to the result by incrementing the entry’s count, so the invariant holds.

If the entry’s value isn’t the same as the new value, we have to push a new entry with the current value and a count of 1.

Showing that this maintains the invariant is the same as when the result list is empty.

Here’s the full function:

Reality Check

Would I really write the RLE function like this? Yes and no.

Yes, in that I would definitely think about the invariant. I’d most likely not need to write anything down; this style of partial_result + what’s left = expected answer is so common it would just seem obvious. However, for more complex cases, I would definitely write down the values of a couple of iterations to help me discover an invariant.

No, in that I’d never write a loop with an index variable which was incremented like this. In a language where control structures return values, I’d very likely write this using values.reduce(). In JavaScript, having to use return bugs me, so I might just write it using a regular iterator, depending on the day.

Takeaway

Ninety percent of the time, I write loops using higher-order functions, and typically don’t need to worry about invariants. But when the going gets gnarly—when I find myself worrying about a condition being correct—I reach for the loop invariant technique. I find it both clarifies and simplifies my thinking and my code.

---

Talking about “simplifying my thinking…” My new book, simplicity, just went into beta. It explores way in which you can simplify your own practices at the project, team, and code level.

See it at pragprog.com.

---